ヒストグラム~QC7つ道具~
ヒストグラムとは
ヒストグラムはQC7つ道具のひとつで, 計量値(量的なデータ:例 kg, m, L, Paなど単位のあるもの)の度数分布を棒グラフで表したものです. 度数を表した長方形(柱)を並べることで, 分布の形を可視化することができます.
規格に対して偏りがないかということや,中心値はどこか, 外れ値はないかといったことを図から目視で確認できるのです.
ヒストグラムでは横軸にデータの数値, 縦軸に度数(データ数)をとり, 縦に長方形を並べた形で表します.
長方形(柱)同士を隙間なく配置するように表示します.
JISではヒストグラムはこのように定義されています.
JIS Z 8101-1
計量値の度数分布のグラフ表示のひとつ. 測定値の存在する範囲をいくつかの区間に分けた場合, 各区間を底辺とし, その区間に属する測定値の度数に比例する面積を持つ長方形を並べた図.
ヒストグラムで使う用語
ヒストグラムを見る際と作る際に使う用語を示します.
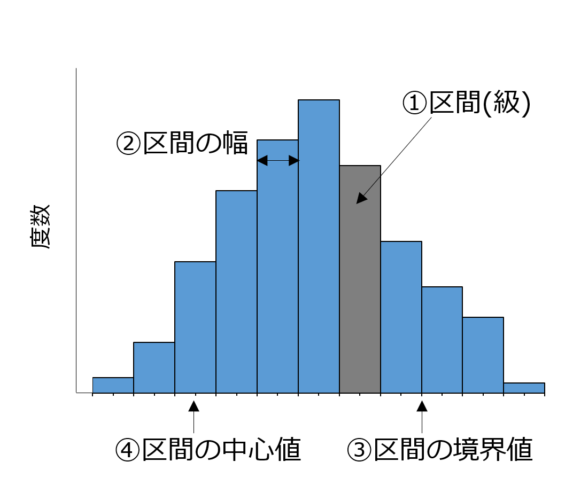
- ① 区間(級) … 測定データをある大きさで区切ったデータ範囲, 級・クラスともいいます.
- ② 区間の幅 … 一つの区間の幅. データの (最大値-最小値)を全部の区間の数 (下の図では11区間)で割ったもの.
- ③ 区間の境界値 … 区間と区間の境目の値
- ④ 区間の中心 … 区間の中心値. 区間の (下側境界値+上側境界値)を2で割ったもの.
- ⑤ 度数 … 区間に分けた測定データの出現度数
- ⑥ 度数分布 … 各区間に属する測定データの出現度数を並べたもの
度数というのは, 特性値のある区間のデータがいくつあるかということです.
ヒストグラムではこの度数が縦軸になります.
ヒストグラムの作り方
手順1 データの収集を行います.
受入検査や製造工程から無作為に計量値データを取ります.
手順2 データの中の最大値と最小値を求めます.
手順3 区間の数を決めます. 区間の数はデータ数の平方根 √nにします.
小数点以下になった場合は最も近い整数値に丸めます.
手順4 区間の幅を決めます.
- 仮の区間の幅 = データの (最大値-最小値)を区間の数 で仮の区間の幅を算出します.
- 測定データの最小数値きざみに掛け合わせると, 最も仮の区間の幅に近づく整数値を選びます.
- (最小数値きざみ:データの最小測定単位, データが小数点第一位まで出ている場合は0.1, 第二位までの場合は0.01)
- 最小数値きざみ×選んだ整数値が区間の幅です.
手順5 区間の境界値を求めます.
区間の境界値は, 測定のきざみの半分 (1/2)のところに来るように決めます.
第1区間の下限境界値 = 最小値 – 測定のきざみ/2
第1区間の上限境界値 = 第1区間の下限境界値 + 区間の幅
手順6 区間の中心値を求めます.
区間の中心値 = (区間の下限境界値 + 区間の上限境界値) /2
手順7 同様に最終区間まで, 中心値と境界値を求めていきます.
手順8 各区間に含まれるデータの数(度数)を数えます.
手順9 中心値 (横軸)と度数 (縦軸)から表計算ソフトでヒストグラムを作成し, 平均値や規格値がある場合には上限規格と下限規格を記入します.
ヒストグラムの見方
一般のヒストグラムの度数は中心付近が最も高く, 中心に対し左右に離れるほど小さくなっていきます.
この分布の形状は, その工程がどのような状態にあるかによっていくつかのパターンに分類できます.
①一般型
データが中心付近に集まっておりひとつの山のようになっている一般的な形で,
工程が管理された状態のときにできる分布です.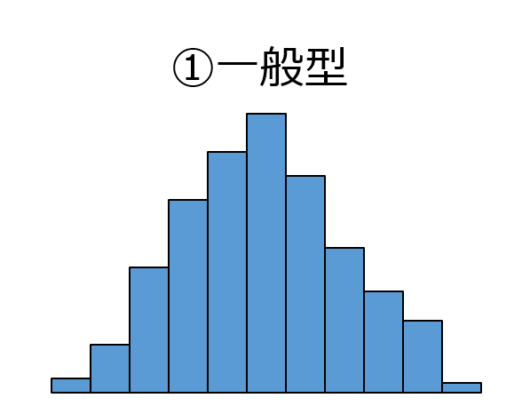
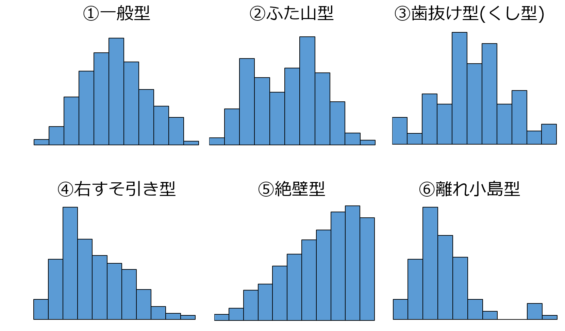
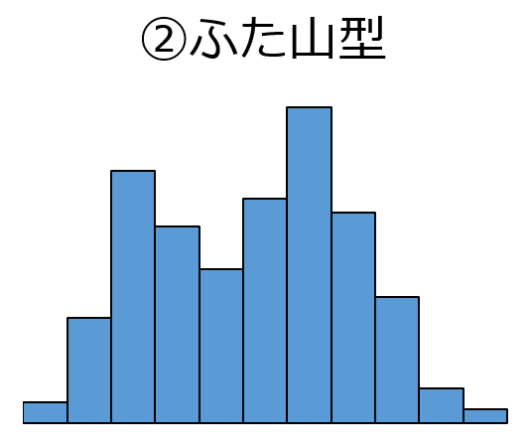
②ふた山型
データが集中している山が2つあります.
ふた山型では分布(平均値)の異なる2種類のデータが含まれていることが考えられるため, 層別が必要です.
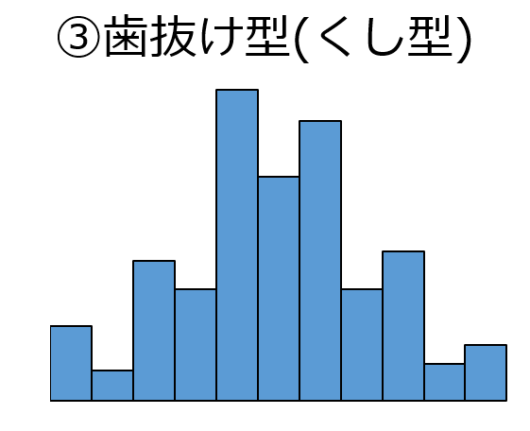
③歯抜け型(くし型)
歯抜け型ヒストグラムは区間幅の取り方が良くない場合や, データ採りや測定にクセがある場合に発生します.
この傾向が見られた場合, データ採取方法やヒストグラム作成の方法を再検討する必要があります.
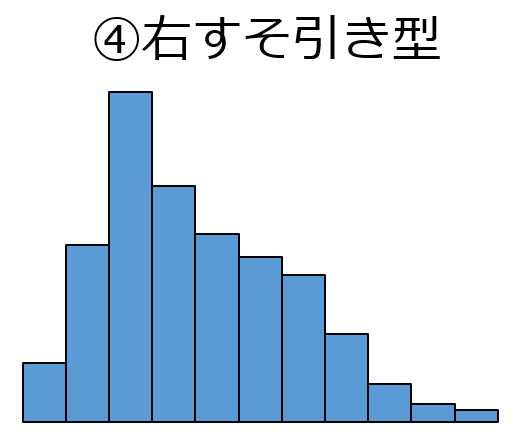
④右すそ引き型 (左右非対称)
データが下限規格付近にに偏っておりすそが右方向へ引いている状態です.
規格外れが出やすいので平均値を上げる対処が必要です.
逆にデータが上限側に集中している場合は左すそ引き型になります.
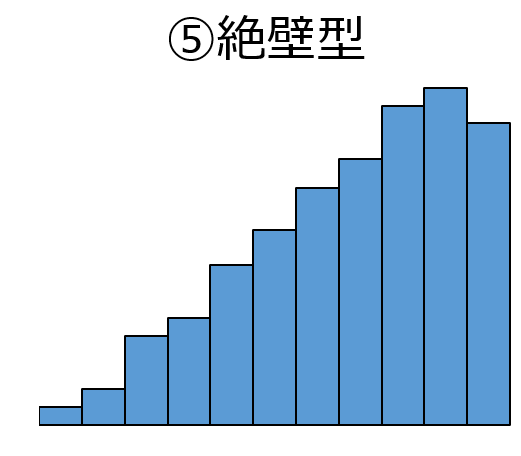
⑤絶壁型ヒストグラム
右(左)端のある部分から急に度数が無くなっており, 絶壁のようになっているヒストグラムです.
規格外(この場合は上限規格)のものを取り除いた場合などに見られます.
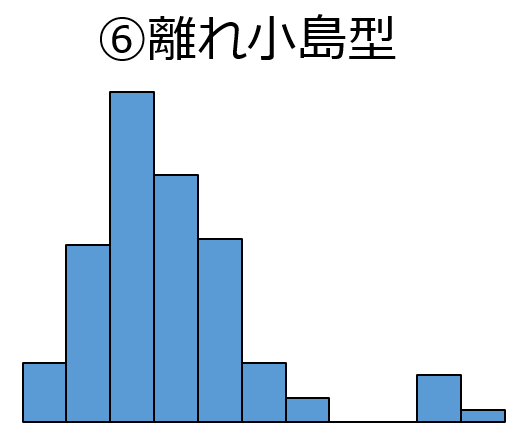
⑥離れ小島型
離れ小島型ヒストグラムでは, データが飛んで現れている箇所があるため,
測定に誤りがないかということや工程に異常がないかを確認する必要があります.
規格値との比較
このようなヒストグラムの分布の形と仕様の規格値を比較することで,
現在の工程の状況が仕様規格を十分に満足することができるかを把握することができます.
ヒストグラムを作成したらデータから工程能力指数を求め規格をどの程度満たすかの確認も併せて行うと効果的です.
ヒストグラムでは分布の形以外にも分布の中心部分の位置, データのばらつきも重要な要素です.
規格値と比較する際は, 分布の中心部分が規格値の中心付近にあるかということや,
ばらつきの大きさは規格値に対して許容できるものかということも考慮します.



















 メーカーで製造技術・品質管理に従事し, 社内研修の講師をしています.
twitter(
メーカーで製造技術・品質管理に従事し, 社内研修の講師をしています.
twitter(