検定・推定とは?帰無仮説・対立仮説【統計学・品質管理の基本】

検定とは
検定とは, 母集団の分布に関する仮説を統計的に検証するものです.
母集団からランダムにサンプル(標本)を採取し, そこから統計量と呼ばれる指標を計算します.
出てきた統計量から, 最初に立てた仮説が正しかったか誤っていたかを判定します.
統計的検定の母集団とサンプル(標本)の関係は下の図のようになります.
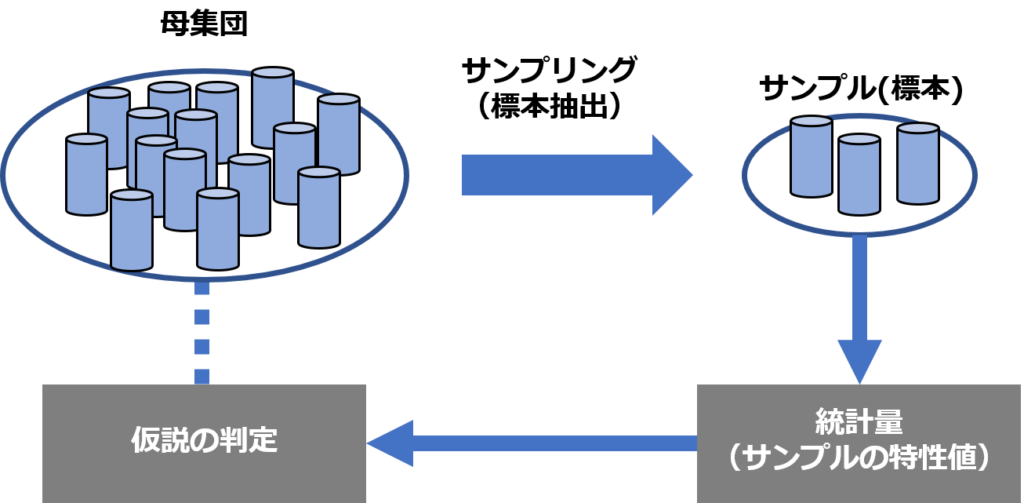
このとき立てる仮説として, 帰無仮説・対立仮説という二つの仮説を立てます.
検定においては, まず立証したいことを対立仮説H1に置き, これを否定する仮説を帰無仮説H0として置きます.
対立仮説には両側仮説と片側仮説があり, それぞれの検定を両側検定, 片側検定といいます.
対立仮説H1:立証したいことを対立仮説に置きます.
帰無仮説H0:対立仮説を否定する仮説を帰無仮説H0として置きます.
帰無仮説H0が真であるにも関わらず, 対立仮説H1が正しいと誤って判断してしまうことを,
第1種の誤り又はあわてものの誤りといい, この確率は有意水準と呼ばれます.
有意水準は記号αで表されます.
第1種の誤りが起こる確率は設定した有意水準となるため,
有意水準の確率が高いほどその危険性が増えてしまいます.
そのため有意水準αの設定値には1%又は5%といった小さい値が一般的に良く用いられます.
それとは逆に, 対立仮説H1が真であるにも関わらず,
帰無仮説H0が正しいと判断してしまう誤りは第2種の誤り又はぼんやりものの誤りと呼ばれます.
その場合の確率は記号βで表します.

検定では, 対立仮説(立証したい仮説)が真のときにそれを正しく検出できることが重要です.
この確率は1-βで表され検出力と呼ばれます.
検定では, データから計算して求めた検定統計量の値が棄却域に入ったときに帰無仮説を棄却し,
対立仮説が成り立つという判断をします.
棄却域とは帰無仮説を棄却すると判断する統計量の範囲のことです.
推定とは
推定とは, 対象とする母集団の分布の母平均や母分散といった母数を推定するものです.
ひとつの推定量により母数を推定する点推定と, 区間を用いて推定する区間推定があります.
区間推定は, 推定値がどのくらい信頼できるかを区間の幅を用いて推定する方法です.
真の母数をその区間に含む確率が設定した信頼率(1-α)となる区間(信頼区間)を推定します.


















 メーカーで製造技術・品質管理に従事し, 社内研修の講師をしています.
twitter(
メーカーで製造技術・品質管理に従事し, 社内研修の講師をしています.
twitter(